Facebook, evidently searching for masses of programmers to do their evil bidding, has actually found a great way to attract engineers at the same time as screening potential job applicants: programming puzzles.

Problem: (the full text of the long-winded setup to the problem can be found after the jump @ facebook)

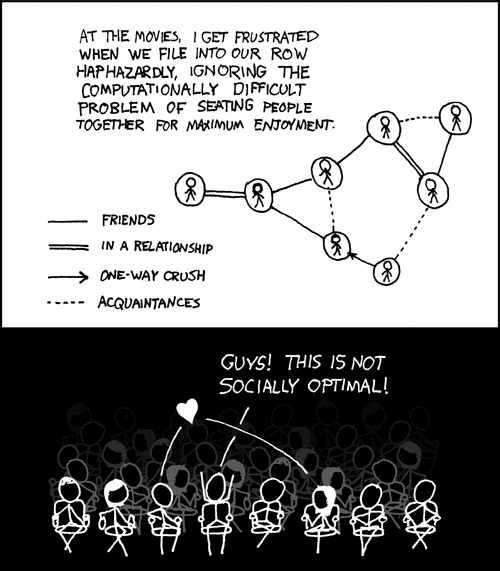
Suppose you and 15 friends are at the cinema to see a long-awaited movie concerning velociraptors, but there is an extremely complex web of social relationships among your group and everyone has to sit together in a single row. As you’re from Cornell you’ll most certainly want to optimize the seating arrangement so that the you maximize the total social welfare of the entire group (i.e. maximize the sum of the payoffs incurred as a result of the seating arrangement).

The social relationships can be defined in a directed graph, with nodes representing people and directed edges representing how one a person feels about another. Types of relationships defined below such as “Mutual Strangers” can be extrapolated across the common edges shared by the relevant nodes. Also, for clarification, an edge which leaves a node1, representing person1, and entering node2, representing person2, and attached with a relationship type implies that person1 has that specific relationship type with person2 and seating them next to each other has a payoff that is dependent on this edge’s relationship type as well as the corresponding reversed edge’s relationship type. Hence, in terms of payoff, we can represent the problem as an undirected graph with each edge weighted with the payoff for seating two node/people adjacent to one another. Also note that this graph is fully connected, as every node has some type of a relationship with every other node.

Relationship types:·

Friends (F) · In A Relationship (R) · One-Way Crush (C) · Acquaintances (A) · Mutual Strangers (S) · Enemy (E) Each one-way pair between two people has only one of these relationship types, listed in the large array below.

Social enjoyment point values:

· 1 pt: Seating acquaintances next to each other · 2 pts: Seating two friends next to each other · 3 pts: Seating two people in a relationship next to each other · 1 pt: Seating someone next to their crush (if the crush is non-mutual) · 0 pt: Seating someone next to someone who has a crush on them · 4 pts: Seating two people together who have mutual crushes on each other · 0 pts: Seating someone next to a person they are strangers with · -4 pts: Seating mutual enemies next to each other · -3 pts: Seating two people in a relationship not next to each other and between them there is someone with a crush on one of them · -2 pts: Seating two people in a relationship not next to each other but between them there are no people with a crush on either of them · -2 pts: Seating someone not next to their crush but with that person’s significant other between them and the crush · -1 pts: Seating someone surrounded by strangers

Relevance:

Defining the optimum linear connection among a group of objects or people comes up pretty much constantly in everything from Operations Research to seating one’s extended family without fear of grievous bodily injury. Using the concept of social networking provides a nice framework to analyze the more complex graph theory going on under the surface, and maximizing the total payoff across a group is a serious topic in economics, with the small caveat that in this problem the people are not independent agents playing for their own welfare but rather being assigned to their seats. An interesting tangent would be to find the nash equilibrium if all the people were acting as independent agents.

So - This is Hard, NP-Hard

What we, in effect, have found is a nifty instance of a traveling salesman problem (TSP). This is a problem described by a situation where a salesman needs to visit a given set of cities (nodes), there is a cost traveling from one to another equal to the distance between the cities (weighted edges), and each node can only be traveled once. We can think about people as different cities and the relative payoff between two people akin to the cost of traveling between them. For this general problem, finding an optimal solution is np-hard (i.e. no fast algorithm which guarantees optimality and need to enumerate all solutions) and even asking if given a solution S is there a different solution S’ with a bigger payoff/less distance traveled is np-complete (i.e. good luck trying to find a solution to this).

An interesting graphical representation of this can be described as finding a Hamiltonian Circuit among a graph.

What do we do, then? Well, for more hefty solutions, this problem is mostly worked on by using a hybrid of two algorithm types: branch-and-bound, a linear programming (optimization) tool and a pruning method resembling a class of algorithms called Genetic Algorithms, which start off with a large search space then use a heuristic to prune some of the solutions that don’t seem to be promising.

For our small subset of the larger space of the problem, we can just use Branch-and-Bound:

1. We change the payoffs so that they are in the form of costs, with 0 cost on an edge representing 4pts of seating two mutual crushes together and 8 the cost of seating mutual enemies together
2. We divide the problem into a number of subproblems
3. To avoid computation over all possibilities, we try to find a viable solution first and use its cost as an upper bound for the optimum. All future calculations are terminated as soon as their costs exceed the costs of the upper bound
4. If a cheaper solution is found, its value is used as the upper bound
5. In this way, many calculations that would have to be done can be stopped early on.

Algorithm:

Enumerating all combinations, 16 seats with 16, 15, 14 … 2, 1 options for people in each seat if we iterate through them would leave us with 16! (16 factorial: 16 * 15 * … * 1) possible combinations, and analyzing 2.0923e+013 solutions for cost would work, although probably not get you a job at Facebook anytime soon.

So, what do we want?

1. Valid Seating: all 16 seats must be filled with different people
2. Maximum Payoff: sum of payoffs of social enjoyment values for adjacency is maximized

What do we have?

1. 16 nodes
2. 136 edges: can think of first node having 15 shared edges, second having 14 shared edges (as node to first already used), and so on

What do we do?

Using our branch and bound class of algorithm with our payoffs modified into a cost structure we come up with:

1. Choose an arbitrary start node as current node
2. Set upper bound to infinity (or max_double for geeks)
3. Choose cheapest edge between current node and an unvisited node, Add cost of edge linking the two to a value of currentCosts and repeat until either currentCosts > bound and sequence of nodes has not been completed or we have a valid seating
4. if currentCosts < upperBound, set this seating as the min seating and the upper bound as the cost of this trip
5. set the current path as something to never try again
6. Repeat until done or until we are satisfied enough with our solution

So, we can either wait for an optimum, which might take a while to find or we can terminate early with probably a pretty good seating arrangement. woohoo!